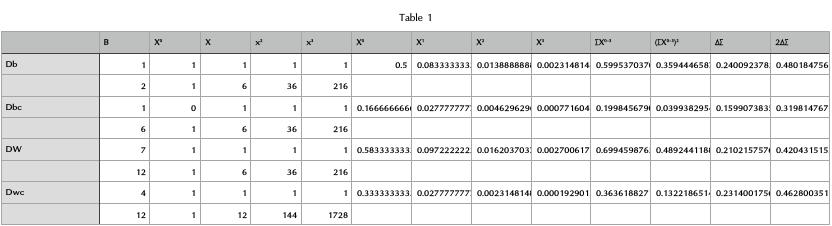
I thought it could be interesting to have a place to discuss mathematical probabilities in the game. It would surely help me in running my game and doing my houserules!
for example, what do you think is the harsher penalty on a check (the penalty which is most likely going to make you fail the check);
+1 to the TN
or
a disadvantage (reroll 2 dice containing success/explosion).
if anybody did some charts or calculation for the dices in this game, leave it here !
Given that
Mathematically speaking, they're about (note not exactly) equal until compromised. Then the TN penalty is MUCH worse.
whence compromised, they're FAR worse.
Heading for the spreadsheet. I'll insert the results shortly.
Per die, expected successes
Black ≅ 0.599537037037037
Black Compromised = 0.199845679012346
White = 0.69945987654321
White Compromised = 0.363618827160494
one reroll
B 0.359444658779149
BC 0.0399382954199055
W 0.489244118893843
WC 0.132218651465573
So the reroll costs about 0.24 on an uncompromised die. Two rerolls deprives about half a success. TN 1 kills a success.
It gives a rough idea! Thx! Obviously the reroll gives you a chance of dropping a success for an explosion but that should be only a very slight probability change.
I was looking to apply some "penalty" on some check without being harsh enough to raise the TN. A bit like star wars blue dice, which I really like for general purpose.
If I want to follow the game's pattern, a disadvantage is logical.
So, because of a "situation" or whatever else, like, when attacking from prone (which was my original intent with this post), I am being nicer by giving a disadvantage instead of a +1tn.
do you also think the opposite is true?
Than an advantage is worst than a -1tn?
Since you can choose which dice to reroll with an advantage it makes the calculation difficult! But considering you would reroll a non success to try to get a success, about +.5 success per advantage is maybe a good go to. So a -1tn is better (I think?)
This ties to a similar question: which is more worthwhile between spending a Void point to seize the moment or to invert/exploit a disadvantage (yours or theirs, respectively)?
My intuition is that this also depends on your dice pool and the rolled/kept ratio, no? If you roll a lot and keep significantly fewer dice, then rerolling successes won’t hurt you as much, but a +1 TN will hurt you just the same?
Two dice rerolled drops your expected successes, pretty much in all conditions, by 0.38 to 0.48... A -1 TN is thus equivalent to between 4d and 5d
The X referred to is the recursion rate - that is, how many explosives in a row. The ∆ is the difference between non rerolled and rerolled.
If uncompromised, the reroll costs just under half a success expected with either die type; the TN+1 is –1 success. The TN penalty is always stronger than a 2d reroll.
Now, as to Franwax's question
Rerolling 2d is +0.32 to +0.48
Adding another is +0.2 to +0.7 — If compromised, reroll. If not, extra die
12 hours ago, AK_Aramis said:whence compromised, they're FAR worse.
Thanks! It's a well-explained analysis.
I have a few assessments I've done on the back of a spreadsheet but they're nowhere near as elegant.
A couple of qualitative (rather than numerical) notes:
Also worth noting is the balance between ring and skill die. Whilst the two aren't massively different in average rolls, the big difference comes when you're compromised (or unwilling to take strife results because you're trying to avoid becoming so), because the skill die still has only 3 strife results (making them half as likely).
Most critical is the fact that the ring die has a strife on its explosive success result.
That means that unless assistance or void points add bonus dice, a compromised character attempting an unskilled check has zero chance whatsoever of passing any check with a TN higher than the ring being used.
By comparison, a skilled, compromised character still has about 1/2 the dice results 'open', including both a success/opportunity and an explosive success.
Added to the fact that being skilled adds a rolled but not a kept die, having one or two ranks of a skill isn't that powerful for 'day job' tasks.
They really come into their own for checks where you are compromised or absolutely positively must get at least one 'double result' to have a chance of success (a ring 3 character trying to inflict a critical strike with a successful strike action springs to mind)
I did some test dice rolls a while ago to get a feel for the basic TN probabilities. The data were gained from rolling each dice pool 100 times and recording the results; the probabilities are the chance of making at least that TN and have been rounded to the nearest 5% or 33%/66%. Missing TNs have 0% chance. Because this was from a small sample size, there may be some anomalies and deviations from the true probabilities.
Strife and opportunities were ignored, the only goal was the highest TN. While I didn't record strife or opportunities, there were definitely a lot more choices with the dice pool with more skill dice. High skill dice rolls make it much easier to meet lower/medium TNs with minimal strife / max opportunities, as well as making it easier to make higher TNs.
No Skill Dice
1k1. TN 0, 50%. TN 1, 50%. TN 2, 30%.
2k2. TN 0, 20%. TN 1, 80%. TN 2, 33%. TN 3, 10%.
3k3. TN 0, 15%. TN 1, 85%. TN 2, 50%. TN 3, 20%. TN 4, 5%.
One Skill Die
2k1. TN 0, 15%. TN 1, 85%. TN 2, 20%. TN 3, 5%.
3k2. TN 0, 5%. TN 1, 95%. TN 2, 66%. TN 3, 30%.
4k3. TN 0, 5%. TN 1, 95%. TN 2, 80%. TN 3, 50%. TN 4, 15%.
Two Skill Dice
4k2. TN 0, 5%. TN 1, 95%. TN 2, 75%. TN 3, 25%. TN 4, 5%.
5k3. TN 0, 0%. TN 1, 100%. TN 2, 85%. TN 3, 66%. TN 4, 40%.